There are a lot of cool weapons in Arkane Studios’ latest FPS, all of which are divided into colored tier levels that indicate their quality. Typically, purple is the best, but there are a handful of gold-colored weapons that are the very best in the game. Here we’ll explain how to get the Heritage Gun in Deathloop, a powerful shotgun with two separate firing modes. It’s a rather tricky and longwinded process but totally worth it.
How to Get the Heritage Gun in Deathloop
As mentioned above, getting the Heritage Gun is a rather long process, and that’s because you will have to beat three separate and rather difficult puzzles to get it.
First things first, head to Karl’s Bay in the evening. As soon as you exit the tunnels take a right and then jump up above the wall beside you and look down to observe two Eternalists opening a present that then explodes. This alludes to your task ahead.

Continue down the road and approach the building signed ‘Fathoms of Lament.’ Take out the Eternalists inside, then note the large map with shining buttons. These represent presents scattered around Karl’s Bay like the one you saw the Eternalists opening before. To get the Heritage Gun you will need to open all of them, turning the light from blinking white to solid blue. Once all the presents are open and all the lights are solid blue you will be able to take part in the final puzzle inside ‘Fathoms of Lament’ itself.

As you will have noticed, one or two of the lights are already solid blue. The locations of the others are random for each game, but two remain the same: one in the centre-left and the other in the top-right of the map. These represent the puzzles we’ll help you solve below. Before you tackle them, though, go and open the other presents around Karl’s Bay. Beware, though, while some of them will reward you with Trinkets and other goodies, others will explode. Be sure to always run away after opening one just in case.

Now onto the first puzzle. Go to the present represented by the centre left white blinking light. This is a nightclub called Dawn of Reason. It has a lever outside, but this will only open the door for a limited amount of time, and you’re going to need much more than it allows. So, instead, go around to the right of the building and jump up into the window.
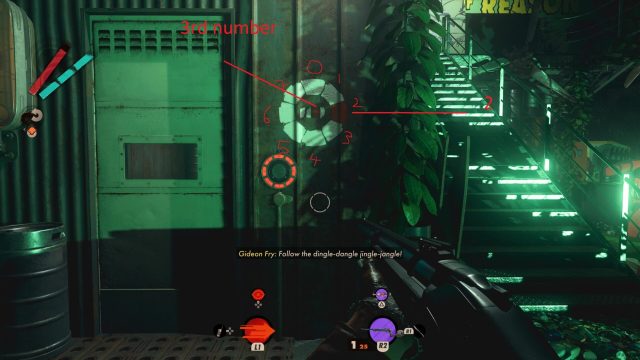
Once inside, drop down to the bottom level and find the locked door at the back. To open this door you will need to input a sequence of four numbers. The numbers are random for each game, but the puzzle is the same. Spray painted around the club in random locations are circular symbols with red and white lines inside that represent the numbers you need to enter. There is always one right beside the lock itself, and it is the easiest to use as a blueprint to understand how the puzzle works.
The red line in the middle of the circle represents the sequence, while the red block on the outside corresponds to the number on the keypad. So, looking at the example above, the painting is telling us that the third number is 2 (the very top white block on the dial is 0).

Now you need to go and find the other spray-painted symbols. Some require you to stand at various angles to line up, while one is always partially obscured and forces you to guess as to which of three numbers it’s likely to be. Don’t worry, it’s easy once you get the hang of it — just use a pen and paper to write down the numbers as you find them.
Right, now onto the next puzzle. This one takes you to Hanger 2 in the top right-hand corner of Karl’s Bay. You should remember it as where you killed Harriet. Well, now it’s totally empty except for the present you need to open. But it’s not that easy; there are six levers here you need to pull to unlock it in a special sequence, and after you pull the first lever you only have 30 or so seconds to get the order correct.
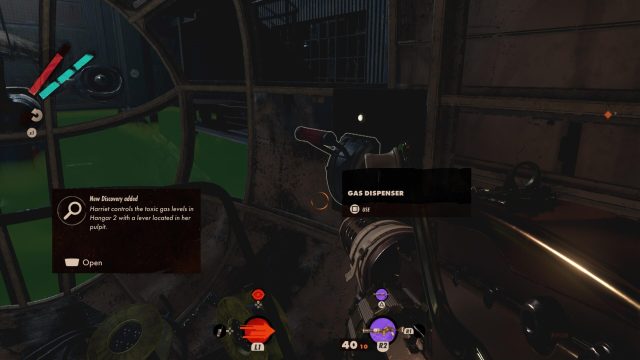
Before you begin, go into Harriet’s office and pull the lever in her office to remove most of the toxic gas from the room. It just makes things easier. It’s in the glass turret that protrudes from her office where she gives her speech when visiting Karl’s Bay in the morning.
Right, now it’s time to pull the levers. Before you get started, go to the first one (besides the present) and observe where the other five are. There’s one opposite, one below you, one to your right, one on the plane, and one over in a far (and very dark) corner that is hard to see. Make a mental note of where they are, then pull the lever. You will know which ones to pull as there is an audio cue that sounds like a loud ticking sound when you get close to the correct one.
It may take one or two tries to get the sequence correct, but it’s not overly difficult. After you’re done, open the present, though obviously be careful it isn’t explosive!

Now it’s time to return to ‘Fathoms of Lament’ and play out the final puzzle. You will notice now that there is a door towards the back-right of the room which is now open. Go through and notice there’s a lever here. That’s right, it’s another timed lever puzzle!
The idea is the same as before, though this time there are Field Nullifiers that remove your ability to Shift, and lasers that will cancel the timer if you touch them. When you’re ready, pull the lever, then run up the stairs and begin navigating around the room pulling the levers in the correct order. The order may be random between each game, but either way we found that there are one or two spots you can use still use Shift to speed up your run.
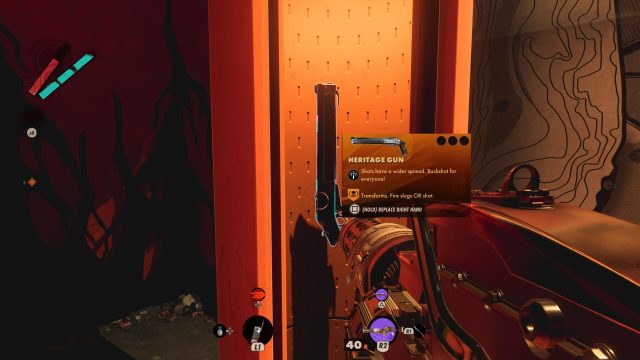
After you have completed the puzzle you will have access to the precious Heritage Gun. Happy shootin’!
That’s everything you should need to know about how to get the Heritage Gun in Deathloop. For more tips and tricks on the game, do be sure to check out Twinfinite’s detailed wiki page. You should also see some related content below that may prove useful.
If you can’t find an answer to a specific question you have, though, always feel free to reach out in the comment section below and we’ll do our best to lend a hand.




